Category: 開発

There’re many problems in this world that you have no idea how to solve in a perfect way, but you can at least give it an okay solution. Like, say, how to cook, or how to run. As long as it’s a computational problem, and possible to quantitatively define a score to the ideal state, that’s probably where an evolutionary algorithm comes in.

The key idea of an evolutionary algorithm, often the case with a genetic algorithm as well, is to evaluate the loss of parameter(s) and iterate doing it. And between each iteration, you want to tweak your parameters a little bit. Sometimes you can add random factors, too. Repeating iterations will hopefully lead you to a heuristic solution.

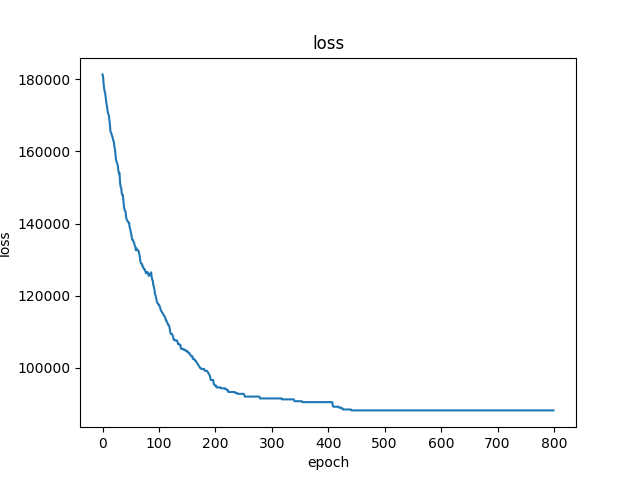
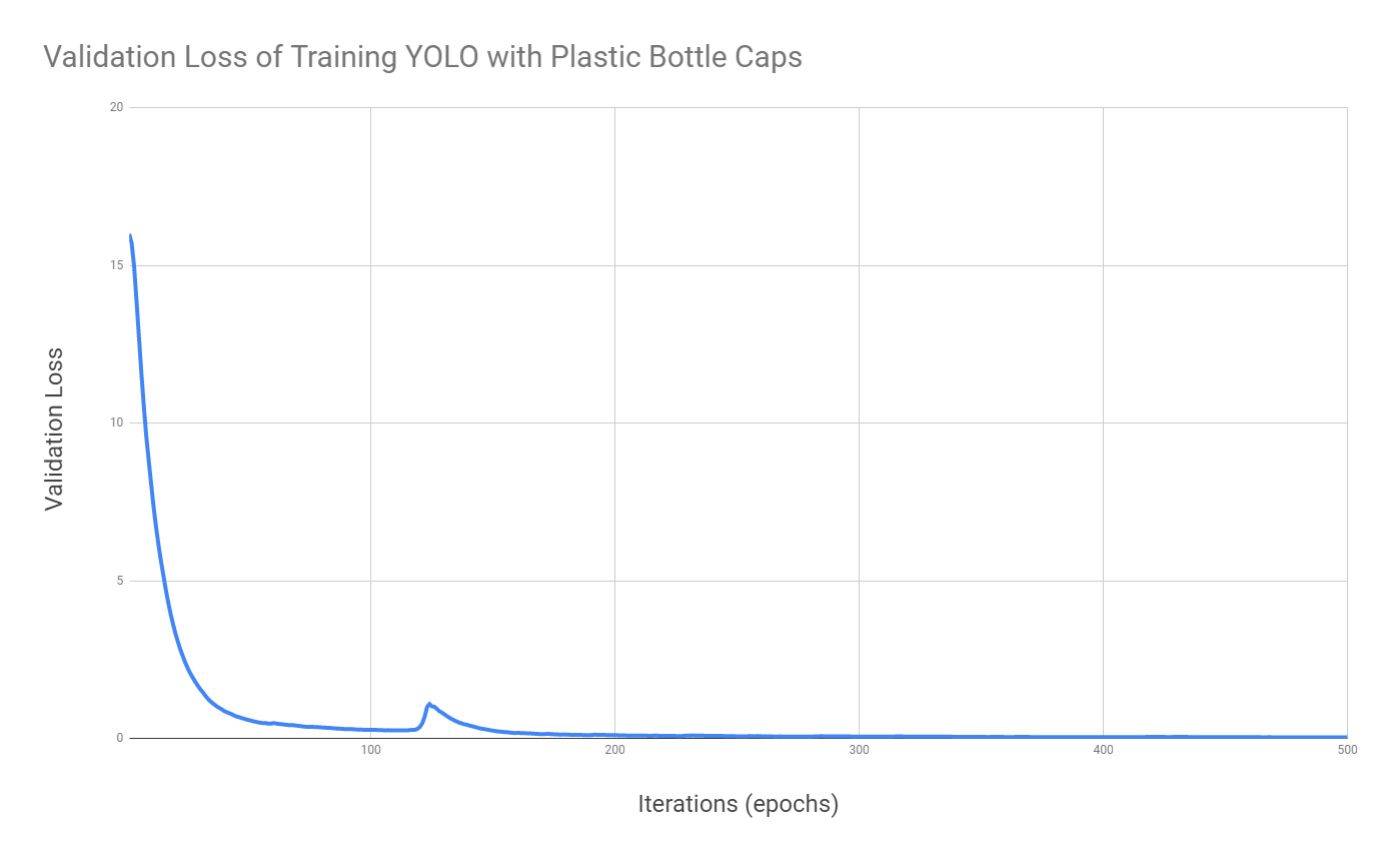
You’re strongly recommend that you plot the loss of your computation so that you can find where to stop it, otherwise your computer will be working for days or weeks.

Here’s how I code to a test problem that is placing circles homogenously in a given area. The dependencies of libraries are not so many because it’s simple enough to write the code from scratch.

And below is the plot of the progress of finding the solution. Where to stop is subject to the project’s resources such as your time or your computational capability.

from PIL import Image, ImageOps, ImageDraw, ImageGrab
import numpy as np
import random, copy, math, time
import matplotlib.pyplot as plt

# consts
fn_image = 'test.png'
c_scatter = 0.005
gen = 1200
radius = 14
c_overlap = 0.675
fn_mask = 'mask64.png'
n_ga_unit = 40
step = 4
n_move = 5

# bounding box around the flood-filled area
def bbox(im):
    im = np.array(im)
    sum_row = im.sum(axis=0)
    sum_col = im.sum(axis=1)
    idx_row = np.where(sum_row>0)
    idx_col = np.where(sum_col>0)
    left = idx_row[0].min()
    right = idx_row[0].max()
    top = idx_col[0].min()
    bottom = idx_col[0].max()
    return (left, top, right, bottom)

def crossover(a, b, idx):
    return (a[:idx]+b[idx:], b[:idx]+a[idx:])

im = Image.open(fn_image)
im = im.convert('L')
objective_size = np.asarray(im).sum()
n_iter = int(c_scatter * objective_size)
bb = bbox(im)

mask = Image.open(fn_mask).convert('L') # greyscale
score_perfect = np.asarray(mask).sum()
score_threshold = int(score_perfect * c_overlap)
mask = ImageOps.invert(mask)
black = Image.fromarray(np.reshape(np.zeros(mask.width * mask.height), [mask.width, -1]))

def score(render, x, y, r):
    im_crop = render.crop((x-r, y-r, x+r, y+r))
    output = ImageOps.fit(im_crop, mask.size, centering=(0.5, 0.5))
    output.paste(black, (0, 0), mask)
    ar = np.asarray(output)
    return (output, ar.sum())

class GAUnit:
    def __init__(self, size):
        self.mod = [None] * size
        for i in range(n_move):
            idx = random.randrange(size)
            self.mod[idx] = random.random()*2*math.pi
        
    def evolve_rand(self):
        size = len(self.mod)
        self.mod = [None] * size
        for i in range(n_move):
            idx = random.randrange(size)
            self.mod[idx] = random.random()*2*math.pi
        
    def evolve(self):
        if random.random() < 0.5:
            self.evolve_rand()
        else:
            for r in self.mod:
                if r is not None:
                    r += random.random() - 0.5 #-0.5 <-> 0.5
    
    def calc_score(self, render, x, y):
        draw = ImageDraw.Draw(render)
        for i in range(len(x_plot)):
            draw.ellipse((x[i]-radius, y[i]-radius, x[i]+radius, y[i]+radius), fill='black')
        self.score = np.asarray(render).sum()
        return render

def iteration(parent, second, third):
    n_crossover = 5
    crossovers = [copy.copy(parent)] * n_crossover
    crossovers[1].mod, crossovers[2].mod = crossover(parent.mod, second.mod, random.randrange(len(parent.mod)))
    crossovers[3].mod, crossovers[4].mod = crossover(parent.mod, third.mod, random.randrange(len(parent.mod)))

    units = []
    for i in range(n_ga_unit-n_crossover):
        u = copy.copy(parent)
        u.evolve()
        units.append(u)
    units = crossovers + units

    for u in units:
        xx = copy.copy(x_plot)
        yy = copy.copy(y_plot)
        for j,deg in enumerate(u.mod):
            if deg is not None:
                xx[j] += step * math.cos(deg)
                yy[j] += step * math.sin(deg)
        u.calc_score(im.copy(), xx, yy)
        
    units.sort(key=lambda x: x.score)
    best = units[0]
    second = units[1]
    third = units[2]
    if best.score < parent.score:
        for j, deg in enumerate(best.mod):
            if deg is not None:
                x_plot[j] += step * math.cos(deg)
                y_plot[j] += step * math.sin(deg)
    return (best, second, third)

# initial plot positions by random
x_plot = []
y_plot = []
render = im.copy()
draw = ImageDraw.Draw(render)
for i in range(n_iter):
    w_bbox = bb[2] - bb[0]
    h_bbox = bb[3] - bb[1]
    x_try = bb[0] + random.randrange(w_bbox)
    y_try = bb[1] + random.randrange(h_bbox)
    (output, s) = score(render, x_try, y_try, radius)
    if s > score_threshold:
        x_plot.append(x_try)
        y_plot.append(y_try)
        draw.ellipse((x_try-radius, y_try-radius, x_try+radius, y_try+radius), fill='black')

# initial parent
unit_size = len(x_plot)
parent = GAUnit(unit_size)
render = parent.calc_score(im.copy(), x_plot, y_plot)
base_score = int(parent.score/10000)
last_score = base_score

scores = None
last_score = base_score
def update_scores(s):
    global last_score, scores
    score_delta = last_score - s
    if not scores:
        scores = [0] * 19
        scores.append(score_delta)
    else:
        scores.append(score_delta)
        scores.pop(0)
    last_score = s

x = []
start = time.time()
best = parent
second = parent
third = parent
for i in range(gen): 
    print('\r{}/{}'.format(i+1, gen), end='')
    best, second, third = iteration(best, second, third)
    x.append(best.score)
    update_scores(int(best.score/10000))
    if sum(scores) == 0:
        step -= 1
        if step < 1:
            step = 1
        n_move -= 1
        if n_move < 1:
            n_move = 1

elapsed_time = time.time() - start
print()
print ("elapsed_time:{0}".format(elapsed_time) + "[sec]")

# result renderring
render = im.copy()
draw = ImageDraw.Draw(render)
for j in range(len(x_plot)):
    draw.ellipse((x_plot[j]-radius, y_plot[j]-radius, x_plot[j]+radius, y_plot[j]+radius), fill='black')
render.save('result.png')

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(np.arange(len(x)), np.array(x))
ax.set_title('loss')
ax.set_xlabel('epoch')
ax.set_ylabel('loss')
fig.savefig('loss.png')

And below is the plot of the progress of finding the solution. Where to stop is subject to the project’s resources such as your time or your computational capability.

Speaking of robotics, in order for a robot to move precisely in the real world, it is essential yet very difficult to set the position and the angle of sensing devices, such as cameras. For this problem, calibration is commonly used, setting the camera’s position and the angle as parameters in a program. But now we have another problem. The difficulty in setting up the camera precisely also means that knowing the camera’s position is also difficult. And the parameter you should know is not only the position but also the angle and the optical features such as FOV(Field Of View) which sometimes isn’t provided by the manufacturer of the sensing device.

Calibration using genetic algorithm

One way to tackle this problem is to use the captured image to assume parameters. And calibration using the genetic algorithm can be one of the easiest solutions.

Let’s say we have a sheet of paper in which a grid pattern is printed, and the camera is seeing it.

We’re reading y-coordinates which the bottom, middle, and top pixel in the image refer to respectively. These values will be used as ground truth for the genetic algorithm.

Just for a sidenote, a simplified diagram of this setup is shown as bellow, which is mathematically easy to describe using tangent equation. The constant we want to know is theta_start, theta_fov, and z.

The greatest advantage of the genetic algorithm is that all you have to do is just to put down the mathematical equation and to give the program the ground truth and then run the program to get the optimal values. Moreover, if the loss of each iteration can be calculated
somehow, the genetic algorithm is likely to work for that problem. So it’s flexible way to search the solutions. Each iteration will evaluate and quantify the fitness of the constants. This is done with the loss function, and least-squares are proper in many cases.

Because the mathematical model, in this case, is continuous, the optimization goes pretty straightforward. If the model complex, you may have to deal with local minima issues.
Otherwise technique required for this optimazation is tweaking the parameters, not using crossover operations.

The code is shown below.

import math, random

def calc_loss(theta_start_in, theta_camera_in, z_in, y_start_in, fac):
    global params

    rand0 = fac * (random.random() - 0.5)
    rand1 = fac * (random.random() - 0.5)
    rand2 = fac * (random.random() - 0.5)
    rand3 = fac * (random.random() - 0.5)
    theta_start = theta_start_in + rand0
    theta_camera = theta_camera_in + rand1
    z = z_in + rand2
    y_start = y_start_in + rand3

    y1 = y_start + z * math.tan(math.radians(theta_start + theta_camera))
    y2 = y_start + z * math.tan(math.radians(theta_start + 0.5 * theta_camera))
    y3 = y_start + z * math.tan(math.radians(theta_start))
    y1_true = params['y1_true']
    y2_true = params['y2_true']
    y3_true = params['y3_true']
    loss = math.pow(y1 - y1_true, 2) + math.pow(y2 - y2_true, 2) + math.pow(y3 - y3_true, 2)
    return loss, theta_start, theta_camera, z, y_start

class Param():
    def __init__(self, loss, theta_start, theta_camera, z, y_start):
        self.loss = loss
        self.theta_start = theta_start
        self.theta_camera = theta_camera
        self.z = z
        self.y_start = y_start

    def __lt__(self, other):
        # self < other
        return self.loss < other.loss

# starter params
theta_start = 1.0
theta_camera = 1.0
z = 1.0
y_start = 1.0

# start learning
n_gen = 500
n_epoch = 2000
for i in range(n_epoch):

    children = []
    for j in range(n_gen):
        factor = 0.01 if j > 0 else 0

        loss_ret, theta_start_ret, theta_camera_ret, z_ret, y_start_ret = calc_loss(theta_start, theta_camera, z, y_start, factor)
        child = Param(loss_ret, theta_start_ret, theta_camera_ret, z_ret, y_start_ret)
        children.append(child)

    # 0th is the best
    children = sorted(children)
    theta_start, theta_camera, z, y_start = children[0].theta_start, children[0].theta_camera, children[0].z, children[0].y_start
    if i == 0:
        print ''
        print 'worst child: loss: {}'.format(children[len(children)-1].loss)
    if i % 500 == 0:
        print 'epoch: {}, loss: {}'.format(i, children[0].loss)

# results
best = children[0]
params['theta_start'] = best.theta_start
params['theta_camera'] = best.theta_camera
params['z'] = best.z
params['y_start'] = best.y_start
data = json.dumps(params, indent=4)
fn = 'camera_params.json'
with open(fn, 'w') as f:
    f.write(data)
    f.close()

print '\nlearned params:'
for k,v in params.items():
    print '{}: {}'.format(k, v)

In each iteration, the best individual, which of cource marked the least loss, is to be picked and used as a parent of the next iteration. The loss value after 2,000 epochs with 500 individuals eventually turned out to be nearly zero. And we got the optimal solutions for this problem.